TensorFlow (2) Classifying MNIST

1. MNIST (Mixed National Institute of Standards and Technology) handwritten digits dataset:

MNIST 是一個泛用的手寫字資料庫，每一筆 MNIST 的圖片代表數字 0 到 9，由 784 個 pixels 組成。我們從資料庫中拿出的資料是 1*784 的一個扁平矩陣。

#!/usr/bin/python3
from matplotlib import pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data

DATA_DIR = 'data'
data = input_data.read_data_sets(DATA_DIR, one_hot=True)

num, ans = data.train.next_batch(1)
print("num.shape: ", num.shape)
print("ans(one_hot): ", ans)

plt.imshow(num.reshape([28,28]))
plt.show()

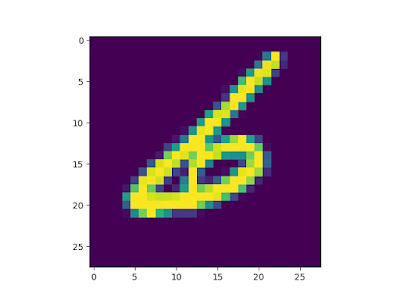
執行結果如下，data.train.next_batch 會回傳一筆資料和答案。one_hot=True 會讓回傳的答案以陣列的形式回傳，並將答案標成 1。num.shape 是矩陣的大小，ans 是圖片的答案。

num.shape:  (1, 784)
ans(one_hot):  [[0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]]

在 plt.imshow 的時候我們把圖片還原回 28*28 的方陣，並用圖片的方式顯示方陣(要看方陣的數值可以 print(num))。

2. 辨識 MNIST:

#!/usr/bin/python3
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

DATA_DIR = 'data'
NUM_STEPS = 1000
MINIBATCH_SIZE = 100

data = input_data.read_data_sets(DATA_DIR, one_hot=True)

# 定義計算
x = tf.placeholder(tf.float32, [None, 784])
W = tf.Variable(tf.zeros([784, 10]))
y_pred = tf.matmul(x, W)

y_true = tf.placeholder(tf.float32, [None, 10])

# 定義誤差
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
                       logits=y_pred, labels=y_true))
gd_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

# 簡單定義正確性
correct_mask = tf.equal(tf.argmax(y_pred, 1), tf.argmax(y_true, 1))
accuracy = tf.reduce_mean(tf.cast(correct_mask, tf.float32))

# 開始訓練
with tf.Session() as sess:
    # Train
    sess.run(tf.global_variables_initializer())
    for _ in range(NUM_STEPS):
        batch_xs, batch_ys = data.train.next_batch(MINIBATCH_SIZE)
        sess.run(gd_step, feed_dict={x: batch_xs, y_true: batch_ys})
    
    # Test
    ans = sess.run(accuracy, feed_dict={x: data.test.images,
                   y_true: data.test.labels})

print ("Accuracy: {:.4}%".format(ans*100))

3. 定義計算:

我們先開一個維度是 n*784 的矩陣 x 再開一個維度是 784*10 的矩陣 W。x*W 會回傳出 n*10 的結果。x*W 的數值代表猜測的答案，數值越大代表我們的模型認為它是答案。

我們先用 softmax normalize 結果再和正解計算 cross_entropy。

4. 定義誤差:

在學習的過程中我們要評估並修正我們的答案，cross_entropy 是我們離正確解答的距離，如果 cross_entropy 越大代表我們離正確解答越遠。

cross_entropy 是一個 W 的函數，而深度學習目的就是找出 entropy 的 minimum (最怕的是 cross_entropy 有多個 minima 或是 minimum 不夠好)。

每次我們猜完答案後會跟正解計算一次 cross_entropy，如果 cross_entropy 越大代表我們要修正的梯度較大，而修正的方向就是梯度的方向。

Reference

[1] Tom Hope, Yehezkel S. Resheff, and Itay Lieder, Learning TensorFlow A Guide to Building Deep Learning Systems , O'Reilly Media (2017)

[2] Nikhil Buduma , Fundamentals of Deep Learning Designing Next-Generation Machine Intelligence Algorithms , O'Reilly Media (2017)